CHAPTER 8
POWER
CHAPTER LEARNING OBJECTIVES
Upon completion of this chapter, you should be able to do the following:
- Define the term "power."
- Determine horsepower ratings.
It’s all very well to talk about how much work a person can do. The payoff is how long it takes him or her to do it. Look at the sailor in figure 8-1. He has lugged 3 tons of bricks up to the second deck of the new barracks. However, it has taken him three 10-hour days—1,800 minutes-to do the job. In raising the 6,000 pounds 15 feet, he did 90,000 foot-pounds (ft-lb) of work. Remember, force x distance = work. Since it took him 1,800 minutes, he has been working at 90,000 ÷ 1,800, or 50 foot-pounds of work per minute.
That’s power—the rate of doing work. Thus, power always includes a time element. Doubtless you could do the same amount of work in one 10-hour day, or 600 minutes. This would mean that you would work at the rate of 90,000 ÷ 600 = 150 foot-pounds per minute. You then would have a power value three times as much as that of the sailor in figure 8-1.
Apply the following formula:
![]()

Figure 8-1.-Get a horse.

Figure 8-2.-One horsepower.
HORSEPOWER
You measure force in pounds, distance in feet, and work in foot-pounds. What is the common unit used for measuring power? It is called horsepower (hp). If you want to tell someone how powerful an engine is, you could say that it is many times more powerful than a man or an ox or a horse. But what man? and whose ox or horse? James Watt, the man who invented the steam engine, compared his early models with the horse. By experiment, he found that an average horse, hitched to a rig as shown in figure 8-2, could lift a 330-pound load straight up a distance of 100 feet in 1 minute. Scientists agree that 1 horsepower equals 33,000 foot-pounds of work done in 1 minute.
Since 60 seconds equals a minute, 1 horsepower is equal to 33,000/60 = 550 foot-pounds per second. Use the following formula to figure horespower:
![]()
CALCULATING POWER
It isn’t difficult to figure how much power you need to do a certain job in a given length of time. Nor is it difficult to predict what size engine or motor you need to do it. Suppose an anchor winch must raise a 6,600-pound anchor through 120 feet in 2 minutes. What must be the theoretical horsepower rating of the motor on the winch?
The first step is to find the rate at which the work must be done using the formula:
![]()
Substitute the known values in the formula, and you get:
![]()
So far, you know that the winch must work at a rate of 396,000 ft-lb/min. To change this rate to horsepower, you divide by the rate at which the average horse can work—33,000 ft-lb/min.
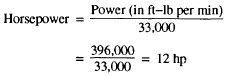
Theoretically, the winch would have to work at a rate of 12 horsepower to raise the anchor in 2 minutes. Of course, you’ve left out all friction in this problem, so the winch motor would actually have to be larger than 12 hp.
You raise planes from the hangar deck to the flight deck of a carrier on an elevator. Some place along the line, an engineer had to figure out how powerful the motor had to be to raise the elevator. It’s not too tough when you know how. Allow a weight of 10 tons for the elevator and 5 tons for the plane. Suppose that you want to raise the elevator and plane 25 feet in 10 seconds and that the overall efficiency of the elevator mechanism is 70 percent. With that information you can figure what the delivery horsepower of the motor must be. Set up the formulas:
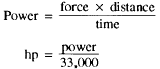
Substitute the known values in their proper places, and you have:
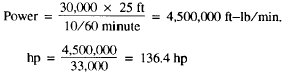
So, you need 136.4 horsepower if the engine has 100 percent overall efficiency. You want to use 70 percent efficiency, so you use the formula:
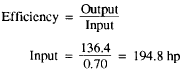
This is the rate at which the engine must be able to work. To be on the safe side, you’d probably select a 200-horsepower auxiliary to do the job.
FIGURING THE HORSEPOWER RATING OF A MOTOR
You have probably seen the horsepower rating plates on electric motors. You may use several methods to determine this rating. One way to find the rating of a
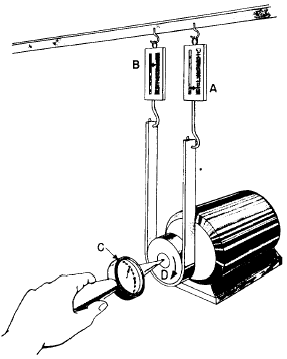
Figure 8-3.-A prony brake.
motor or a steam or gas engine is with the use of the prony brake. Figure 8-3 shows you the prony brake setup. A pulley wheel is attached to the shaft of the motor and a leather belt is held firmly against the pulley. Attached to the two ends of the belts are spring scales. When the motor is standing still, each scale reads the same— 15 points. When the pulley turns in a clockwise direction, the friction between the belt and the pulley makes the belt try to move with the pulley. Therefore, the pull on scale A will be greater than 15 pounds, and the pull on scale B will be less than 15 pounds.
Suppose that scale A reads 25 pounds and scale B reads 5 pounds. That tells you the drag, or the force against which the motor is working, is 25 – 5 = 20 pounds. In this case the normal speed of the motor is 1,800 revolutions per minute (rpm) and the diameter of the pulley is 1 foot.
You can find the number of revolutions by holding the revolution counter (fig. 8-3, C) against the end of the shaft for 1 minute. This counter will record the number of turns the shaft makes per minute. The distance (D) that any point on the pulley travels in 1 minute is equal to the circumference of the pulley times the number of revolutions or 3.14 x 1 x 1,800 = 5,652 ft.
You know that the motor is exerting a force of 20 pounds through that distance. The work done in 1 minute is equal to the force times the distance, or work = F x D = 20 x 5,652 = 113,040 ft-lb/min.
Change this to horsepower:
![]()
Two common motor or engine ratings with which you are familiar are the 1/16-hp motor of an electric mixer and the 1/4-hp motor of a washing machine.
SUMMARY
Remember two important points about power:
Power is the rate at which work is done.
Horsepower is the unit of measurement by which power is equivalent to 33,000 foot-pounds of work per minute, or 550 foot-pounds per second.

Tidak ada komentar:
Posting Komentar