CHAPTER 6
GEARS
CHAPTER LEARNING OBJECTIVES
Upon completion of this chapter, you should be able to do the following:
- Compare the types of gears and their advantages.
Did you ever take a clock apart to see what made it tick? Of course you came out with some parts left over when you got it back together again. And they probably included a few gear wheels. We use gears in many machines. Frequently the gears are hidden from view in a protective case filled with grease or oil, and you may not see them.
An eggbeater gives you a simple demonstration of the three jobs that gears do. They can change the direction of motion, increase or decrease the speed of the applied motion, and magnify or reduce the force that you apply. Gears also give you a positive drive. There can be, and usually is, creep or slip in a belt drive. However, gear teeth are always in mesh, so there can be no creep and slip.
Follow the directional changes in figure 6-1. The crank handle turns in the direction shown by the arrow—clockwise—when viewed from the right. The 32 teeth on the large vertical wheel (A) mesh with the 8 teeth on the right-hand horizontal wheel (B), which rotates as shown by the arrow. Notice that as B turns in a clockwise direction, its teeth mesh with those of wheel C and cause wheel C to revolve in the opposite direction. The rotation of the crank handle has been transmitted by gears to the beater blades, which also rotate.
Now figure out how the gears change the speed of motion. There are 32 teeth on gear A and 8 teeth on gear B. However, the gears mesh, so that one complete revolution of A results in four complete revolutions of gear B. And since gears B and C have the same number of teeth, one revolution of B results in one revolution of C. Thus, the blades revolve four times as fast as the crank handle.
In chapter 1 you learned that third-class levers increase speed at the expense of force. The same happens with the eggbeater. The magnitude of force changes. The force required to turn the handle is greater than the force applied to the frosting by the blades. This results in a mechanical advantage of less than one.
TYPES OF GEARS
When two shafts are not lying in the same straight line, but are parallel, you can transmit motion from
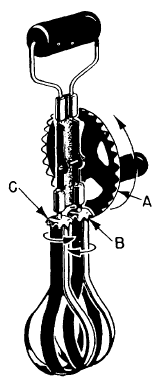
Figurc 6-1.—A simple gear arrangement.
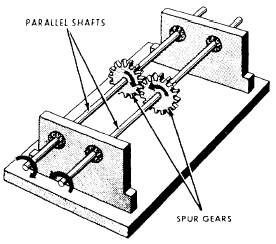
Figure 6-2.4-Spur gears coupling two parallel shafts.
one to the other by spur gears. This setup is shown in figure 6-2.
Spur gears are wheels with mating teeth cut in their surfaces so that one can turn the other without slippage. When the mating teeth are cut so that they are parallel to the axis of rotation, as shown in figure 6-2, the gears are called straight spur gears.
When two gears of unequal size are meshed together, the smaller of the two is usually called a pinion. By unequal size, we mean an unequal number of teeth causing one gear to be a larger diameter than the other. The teeth, themselves, must be of the same size to mesh properly.
The most commonly used gears are the straight spur gears. Often you’ll run across another type of spur gear called the helical spur gear.
In helical gears the teeth are cut slantwise across the working face of the gear. One end of the tooth, therefore, lies ahead of the other. Thus, each tooth has a leading end and a trailing end. Figure 6-3, view A, shows you the construction of these gears.
In the straight spur gears, the whole width of the teeth comes in contact at the same time. However, with helical (spiral) gears, contact between two teeth starts first at the leading ends and moves progressively across the gear faces until the trailing ends are in contact. This kind of meshing action keeps the gears in constant contact with one another. Therefore, less lost motion and smoother, quieter action is possible. One disadvantage of this helical spur gear is the tendency of each gear to thrust or push axially on its shaft. It is necessary to put a special thrust bearing at the end of the shaft to counteract this thrust.
You do not need thrust bearings if you use herringbone gears like those shown in figure 6-4. Since the teeth on each half of the gear are cut in opposite directions, each half of the gear develops a thrust that counterbalances the other half. You’ll find herringbone gears used mostly on heavy machinery.
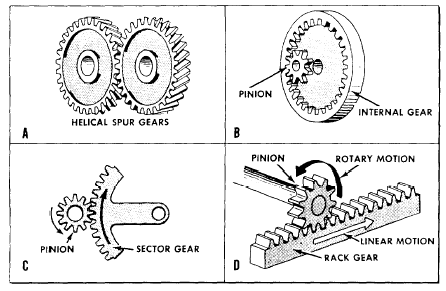
Figure 6-3.-Gear types.

Figure 6-4.—Herringbone gear.
Figure 6-3, views B, C, and D, also shows you three other gear arrangements in common use.
The internal gear in figure 6-3, view B, has teeth on the inside of a ring, pointing inward toward the axis of rotation. An internal gear is meshed with an external gear, or pinion, whose center is offset from the center of the internal gear. Either the internal or pinion gear can be the driver gear, and the gear ratio is calculated the same as for other gears—by counting teeth.
You only need a portion of a gear where the motion of the pinion is limited. You use the sector gear shown in figure 6-3, view C, to save space and material. The rack and pinion in figure 6-3, view D, are both spur gears. The rack is a piece cut from a gear with an extremely large radius. The rack-and-pinion arrangement is useful in changing rotary motion into linear motion.
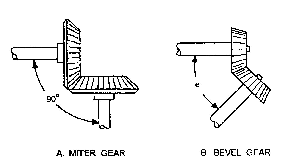
Figure 6-5.-Bevel gears.
THE BEVEL GEAR
So far most of the gears you’ve learned about transmit motion between parallel shafts. However, when shafts are not parallel (at an angle), we use another type of gear called the bevel gear. This type of gear can connect shafts lying at any given angle because you can bevel them to suit the angle.
Figure 6-5, view A, shows a special case of the bevel gear-the miter gear. You use the miter gears to connect shafts having a 90-degree angle; that means the gear faces are beveled at a 45-degree angle.
You can see in figure 6-5, view B, how bevel gears are designed to join shafts at any angle. Gears cut at any angle other than 45 degrees are bevel gears.
The gears shown in figure 6-5 are straight bevel gears, because the whole width of each tooth comes in contact with the mating tooth at the same time. However, you’ll run across spiral bevel gears with teeth cut to have advanced and trailing ends. Figure 6-6 shows you what spiral bevel gears look like. They have the same advantage as other spiral (helical) gears—less lost motion and smoother, quieter operation.
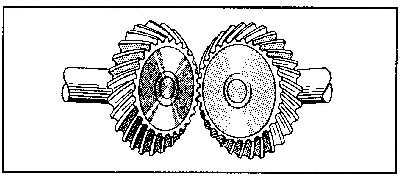
Figure 6-6.-Spiral bevel gears.
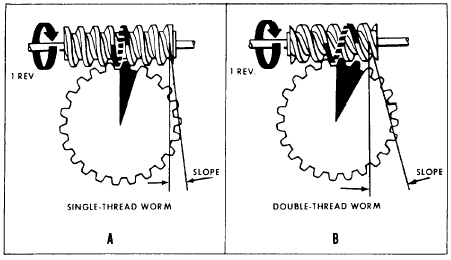
Figure 6-7.—Worm gears.
THE WORM AND WORM WHEEL
Worm and worm-wheel combinations, like those in figure 6-7, have many uses and advantages. However, it’s better to understand their operating theory before learning of their uses and advantages.
Figure 6-7, view A, shows the action of a single-thread worm. For each revolution of the worm, the worm wheel turns one tooth. Thus, if the worm wheel has 25 teeth, the gear ratio is 25:1.
Figure 6-7, view B, shows a double-thread worm. For each revolution of the worm in this case, the worm wheel turns two teeth. That makes the gear ratio 25:2 if the worm wheel has 25 teeth.
A triple-thread worm would turn the worm wheel three teeth per revolution of the worm.
A worm gear is a combination of a screw and a spur gear. You can obtain remarkable mechanical advantages with this arrangement. You can design worm drives so that only the worm is the driver-the spur cannot drive the worm. On a hoist, for example, you can raise or lower the load by pulling on the chain that turns the worm. If you let go of the chain, the load cannot drive the spur gear; therefore, it lets the load drop to the deck. This is a nonreversing worm drive.
GEARS USED TO CHANGE DIRECTION
The crankshaft in an automobile engine can turn in only one direction. If you want the car to go backwards, you must reverse the effect of the engine’s rotation. This is done by a reversing gear in the transmission, not by reversing the direction in which the crankshaft turns.
A study of figure 6-8 will show you how gears are used to change the direction of motion. This is a schematic diagram of the sight mounts on a Navy gun. If you crank the range-adjusting handle (A) in a clockwise direction, the gear (B) directly above it will rotate in a counterclockwise direction. This motion causes the two pinions (C and D) on the shaft to turn in the same direction as the gear (B) against the teeth cut in the bottom of the table. The table is tipped in the direction indicated by the arrow.
As you turn the deflection-adjusting handle (E) in a clockwise direction, the gear (F) directly above it turns
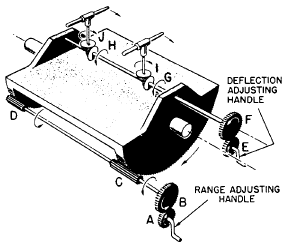
Figure 6-8.-Gears change direction of applied motion.
in the opposite direction. Since the two bevel gears (G and H) are fixed on the shaft with F, they also turn. These bevel gears, meshing with the horizontal bevel gears (I and J), cause I and J to swing the front ends of the telescopes to the right. Thus with a simple system of gears, it is possible to keep the two telescopes pointed at a moving target. In this and many other applications, gears serve one purpose: to change the direction of motion.
GEARS USED TO CHANGE SPEED
As you’ve already seen in the eggbeater, you use gears to change the speed of motion. Another example of this use of gears is in your clock or watch. The mainspring Slowly unwinds and causes the hour hand to make one revolution in 12 hours. Through a series-or train-of gears, the minute hand makes one revolution each hour, while the second hand goes around once per minute
Figure 6-9 will help you to understand how speed changes are possible. Wheel A has 10 teeth that mesh with the 40 teeth on wheel B. Wheel A will have to rotate four times to cause B to make one revolution. Wheel C is rigidly fixed on the same shaft with B. Thus, C makes the same number of revolutions as B. However, C has 20 teeth and meshes with wheel D, which has only 10 teeth. Hence, wheel D turns twice as fast as wheel C. Now, if you turn A at a speed of four revolutions per second, B will rotate at one revolution per second. Wheel C also moves at one revolution per second and causes D to turn at two revolutions per second. You get out two revolutions per second after having put in four revolutions per second. Thus, the overall speed reduction is 2/4—or 1/2—that means you got half the speed out of the last driven wheel you put into the first driver wheel.
You can solve any gear speed-reduction problem with this formula:
![]()
where
S1 = speed of first shaft in train
S2 = speed of last shaft in train
T1 = product of teeth on all drivers
T2 = product of teeth on all driven gears
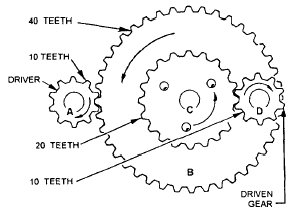
Figure 6-9.-Gears can change speed of applied motion.
Now use the formula on the gear train of figure 6-9.
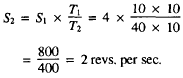
To obtain any increase or decrease in speed you, must choose the correct gears for the job. For example, the turbines on a ship have to turn at high speeds-say 5,800 rpm—if they are going to be efficient. The propellers, or screws, must turn rather slowly—say 195 rpm—to push the ship ahead with maximum efficiency. So, you place a set of reduction gears between the turbines and the propeller shaft.
When two external gears mesh, they rotate in opposite directions. Often you’ll want to avoid this. Put a third gear, called an idler, between the driver and the driven gear. Don’t let this extra gear confuse you on speeds. Just neglect the idler entirely. It doesn’t change the gear ratio at all, and the formula still applies. The idler merely makes the driver and its driven gear turn in the same direction. Figure 6-10 shows you how this works.
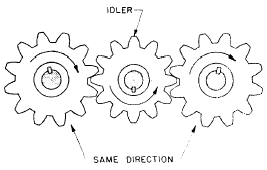
Figure 6-10.-An idler gear.
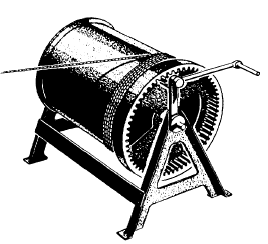
Figure 6-11.-Cable winch.
GEARS USED TO INCREASE MECHANICAL ADVANTAGE
We use gear trains to increase mechanical advantage. In fact, wherever there is a speed reduction, you multiply the effect of the effort. Look at the cable winch in figure 6-11. The crank arm is 30 inches long, and the drum on which the cable is wound has a 15-inch radius. The small pinion gear has 10 teeth, which mesh with the 60 teeth on the internal spur gear. You will find it easier to figure the mechanical advantage of this machine if you think of it as two machines.
First, figure out what the gear and pinion do for you. You find the theoretical mechanical advantage (T.M.A.) of any arrangement of two meshed gears by using the following formula:
![]()
In which,
To = number of teeth on driven gear;
Ta = number of teeth on driver gear.
In this case,
To = 60 and Ta = 10.
Then,
![]()
Now, figure the mechanical advantage for the other part of the machine-a simple wheel-and-axle arrangement consisting of the crank arm and the drum. Divide the distance the effort moves (2pR) in making one complete revolution by the distance the cable is drawn up in one revolution of the drum (2pr).
![]()
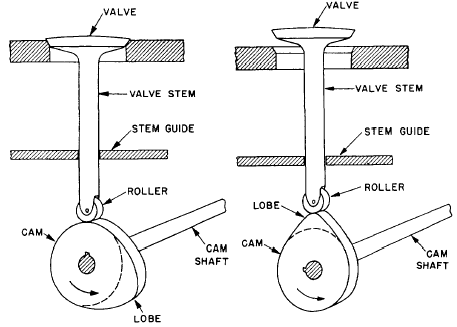
Figure 6-12.-Camdriven valve.
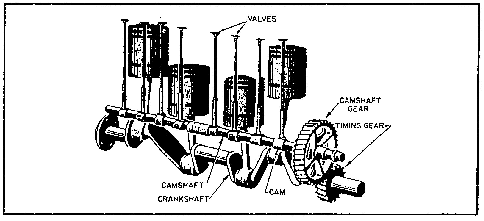
Figure 6-13.—Automobile valve gear.
The total, or overall, theoretical mechanical advantage of a compound machine is equal to the product of the mechanical advantages of the several simple machines that make it up. In this case you considered the winch as two machines— one having a mechanical advantage of 6 and the other a mechanical advantage of 2. Therefore, the overall theoretical mechanical advantage of the winch is 6 x 2, or 12. Since friction is always present, the actual mechanical advantage may be only 7 or 8. Even so, by applying a force of 100 pounds on the handle, you could lift a load of 700 to 800 pounds.
CAM
You use gears to produce circular motion. However, you often want to change rotary motion into up-and-down, or linear, motion. You can use cams to do this. For example, in figure 6-12 the gear turns the cam shaft. A cam is keyed to the shaft and turns with it. The design on the cam has an irregular shape that moves the valve stem up and down. It gives the valve a straight-line motion as the cam shaft rotates.
When the cam shaft rotates, the high point (lobe) of the cam raises the valve to its open position. As the shaft continues to rotate, the high point of the cam passes, lowering the valve to a closed position.
A set of cams, two to a cylinder, driven by timing gears from the crankshaft operate the exhaust and intake valves on the gasoline automobile engine as shown in figure 6-13. We use cams in machine tools and other devices to make rotating gears and shafts do up-and-down work.
ANCHOR WINCH
One of the gear systems you’ll get to see frequently aboard ship is that on the anchor winch. Figure 6-14 shows you one type in which you can readily see how the wheels go around. The winch engine or motor turns the driving gear (A). This gear has 22 teeth, which mesh with the 88 teeth on the large wheel (B). Thus, you know that the large wheel makes one revolution for every four revolutions of the driving gear (A). You get a 4-to-1 theoretical mechanical advantage out of that pair. Secured to the same shaft with B is the small spur gear (C), covered up here. The gear (C) has 30 teeth that mesh with the 90 teeth on the large gear (D), also covered up.

Figure 6-14.—An anchor winch.

Figure 6-15.—A steering mechanism.
The advantage from C to D is 3 to 1. The sprocket wheel to the far left, on the same shaft with D, is called a wildcat. The anchor chain is drawn up over this. Every second link is caught and held by the protruding teeth of the wildcat. The overall mechanical advantage of the winch is 4 x 3, or 12 to 1.
RACK AND PINION
Figure 6-15 shows you an application of the rack and pinion as a steering mechanism. Turning the ship’s wheel turns the small pinion (A). This pinion causes the internal spur gear to turn. Notice that this arrangement has a large mechanical advantage.
Now you see that when the center pinion (P) turns, it meshes with the two vertical racks. When the wheel turns full to the right, one rack moves downward and the other moves upward to the position of the racks. Attached to the bottom of the racks are two hydraulic pistons that control the steering of the ship. You’ll get some information on this hydraulic system in a later chapter.
SUMMARY
These are the important points you should keep in mind about gears:
Gears can do a job for you by changing the direction, speed, or size of the force you apply.
When two external gears mesh, they always turn in opposite directions. You can make them turn in the same direction by placing an idler gear between the two.
The product of the number of teeth on each of the driver gears divided by the product of the number of teeth on each of the driven gears gives you the speed ratio of any gear train.
The theoretical mechanical advantage of any gear train is the product of the number of teeth on the driven gear wheels, divided by the product of the number of teeth on the driver gears.
The overall theoretical mechanical advantage of a We compound machine is equal to the product of the theoretical mechanical advantages of all the simple machines that make it up.
We can use cams to change rotary motion into linear motion.

Tidak ada komentar:
Posting Komentar