Engine Mechanics 7

CHAPTER 7

WORK

CHAPTER LEARNING OBJECTIVES

Upon completion of this chapter, you should be able to do the following:

• Define the term "work" when applied to mechanical power.

MEASUREMENT

You know that machines help you to do work. What is work? Work doesn’t mean simply applying a force. If that were so, you would have to consider that the sailor in figure 7-1 is doing work. He is busy applying his 220-pound force on the seabag. However, no work is being done!

Work in the mechanical sense, is done when a resistance is overcome by a force acting through a measurable distance. Now, if that sailor were to lift his 90-pound bag off the deck and put it on his bunk, he would be doing work. He would be overcoming a resistance by applying a force through a distance.

Notice that work involves two factors-force and movement through a distance. You measure force in pounds and distance in feet. Therefore, you measure work in units called foot-pounds. You do 1 foot-pound of work when you lift a 1-pound weight through a height

Figure 7-1.—No work is being done.

of 1 foot, You also do 1 foot-pound of work when you apply 1 pound of force on any object through a distance of 1 foot. Writing this as a formula, it becomes—

Thus, if you lift a 90-pound bag through a vertical distance of 5 feet, you will do

WORK = 90 X 5 = 450 ft-lb.

You should remember two points about work

1. In calculating the work done, you measure the actual resistance being overcome. The resistance is not necessarily the weight of the object you want to move. To understand this more clearly, look at the job the sailor in figure 7-2 is doing. He is pulling a 900-pound load of supplies 200 feet along the dock. Does this mean that he

Figure 7-2.—Working against friction.

Figure 7-3.—No motion, no work.

is doing 900 x 200, or 180,000 foot-pounds of work? Of course not. He isn’t working against the pull of gravity-or the total weight—of the load. He’s pulling only against the rolling friction of the truck and that may be as little as 90 pounds. That is the resistance that is being overcome. Always be sure you know what resistance is being overcome by the effort, as well as the distance through which it is moved. The resistance in one case may be the weight of the object; in another it may be the frictional resistance of the object as it is dragged or rolled along the deck.

2. You have to move the resistance to do any work on it. Look at the sailor in figure 7-3. The poor guy has been holding that suitcase for 15 minutes waiting for the bus. His arm is getting tired; but according to the definition of work, he isn’t doing any because he isn’t moving the suitcase. He is merely exerting a force against the pull of gravity on the bag.

You already know about the mechanical advantage of a lever. Now consider how it can be used to get work done easily. Look at figure 7-4. The load weighs 300 pounds, and the sailor wants to lift it up onto a platform a foot above the deck. How much work must he do? Since he must raise 300 pounds 1 foot, he must do 300 x 1, or 300 foot-pounds of work.

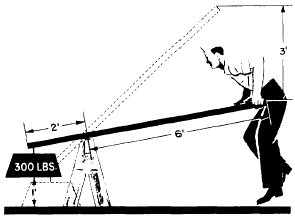
Figure 7-4.—Push’em up.

He can’t make this weight any smaller with any machine. If he uses the 8-foot plank as shown, he can do the amount of work by applying a smaller force through a longer distance. Notice that he has a mechanical advantage of 3, so a 100-pound push down on the end of the plank will raise the 300-pound crate. Through how long a distance will he have to exert that 100-pound push? If he neglects friction, the work he exerts on the machine will be equal to the work done by the machine. In other words,

work put in = work put out.

Since Work = Force x Distance, you can substitute Force x Distance on each side of the work equation. Thus:

in which

F_I = effort applied, in pounds

S₁ = distance through which effort moves, in feet

F₂ = resistance overcome, in pounds

S₂ = distance resistance is moved, in feet

Now substitute the known values, and you get:

1OO x S₁ = 300 x I

S₁ = 3 feet

The advantage of using the lever is not that it makes any less work for you, but it allows you to do the job with the force at your command. You’d probably have some difficulty lifting 300 pounds directly upward without a machine to help you!

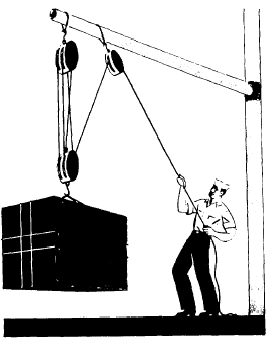
Figure 7-5 - A block and tackle makes work easier

A block and tackle also makes work easier. Like any other machine, it can’ t decrease the total amount of work to be done. With a rig like the one shown in figure 7-5, the sailor has a mechanical advantage of 5, neglecting friction. Notice that five parts of the rope go to and from the movable block. To raise the 600-pound load 20 feet, he needs to exert a pull of only one-fifth of 600—or 120 pounds. He is going to have to pull more than 20 feet of rope through his hands to do this. Use the formula again to figure why this is so:

Work input = work output

And by substituting the known values:

120 x S₁ = 600 x 20

S₁ = 100 feet.

This means that he has to pull 100 feet of rope through his hands to raise the load 20 feet. Again, the advantage lies in the fact that a small force operating through a large distance can move a big load through a small distance.

The sailor busy with the big piece of machinery in figure 7-6 has his work cut out for him. He is trying to seat the machine squarely on its foundations. He must shove the rear end over one-half foot against a frictional

Figure 7-6.—A big push.

resistance of 1,500 pounds. The amount of work to be done is 1,500 x 1/2, or 750 foot-pounds. He will have to apply at least this much force on the jack he is using. If the jack has a 2 1/2-foot handle— R = 2 1/2 feet—and the pitch of the jack screw is one-fourth inch, he can do the job with little effort. Neglecting friction, you can figure it out this way:

Work input = work output

In which

F₁ = force in pounds applied on the handle;

S₁ = distance in feet that the end of the handle travels in one revolution;

F₂ = resistance to overcome;

S2 = distance in feet that the head of the jack advanced by one revolution of the screw, or, the pitch of the screw.

And, by substitution,

F_l x 2 x 3.14 x 21/2 = 1,500 x 1/48

since

1/4 inch = 1/48 of a foot

F₁ x 2 x 2 1/2 = 1,5000 x 1/48

F₁ = 2 pounds

The jack makes it theoretically possible for the sailor to exert a 1,500-pound push with a 2-pound effort. Look at the distance through which he must apply that effort. One complete turn of the handle represents a distance of 15.7 feet. That 15.7-foot rotation advances the piece of machinery only one-fourth of an inch, or one-forty-eighth of a foot. You gain force at the expense of distance.

FRICTION

Suppose you are going to push a 400-pound crate up a 12-foot plank; the upper end is 3 feet higher than the lower end. You decide that a 100-pound push will do the job. The height you will raise the crate is one-fourth of the distance through which you will exert your push. The theoretical mechanical advantage is 4. Then you push on the crate, applying 100 pounds of force; but nothing happens! You’ve forgotten about the friction between the surface of the crate and the surface of the plank. This friction acts as a resistance to the movement of the crate; you must overcome this resistance to move the crate. In fact, you might have to push as much as 150 pounds to move it. You would use 50 pounds to overcome the frictional resistance, and the remaining 100 pounds would be the useful push that would move the crate up the plank.

Friction is the resistance that one surface offers to its movement over another surface. The amount of friction depends upon the nature of the two surfaces and the forces that hold them together.

In many instances fiction is useful to you. Friction helps you hold back the crate from sliding down the inclined ramp. The cinders you throw under the wheels of your car when it’s slipping on an icy pavement increase the friction. You wear rubber-soled shoes in the gym to keep from slipping. Locomotives carry a supply of sand to drop on the tracks in front of the driving wheels to increase the friction between the wheels and the track. Nails hold structures together because of the friction between the nails and the lumber.

You make friction work for you when you slow up an object in motion, when you want traction, and when you prevent motion from taking place. When you want a machine to run smoothly and at high efficiency, you eliminate as much friction as possible by oiling and greasing bearings and honing and smoothing rubbing surfaces.

Where you apply force to cause motion, friction makes the actual mechanical advantage fall short of the theoretical mechanical advantage. Because of friction, you have to make a greater effort to overcome the resistance that you want to move. If you place a marble and a lump of sugar on a table and give each an equal push, the marble will move farther. That is because rolling friction is always less than sliding friction. You take advantage of this fact whenever you use ball bearings or roller bearings. See figure 7-7.

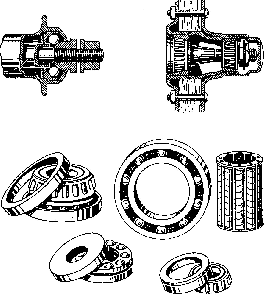
Figure 7-7.—These reduce friction.

Figure 7-8.—It saves wear and tear.

The Navy takes advantage of that fact that rolling friction is always less than sliding friction. Look at figure 7-8. This roller chock cuts down the wear and tear on lines and cables that are run through it. It also reduces friction and reduces the load the winch has to work against.

Figure 7-9.—Roller bitt saves line.

The roller bitt in figure 7-9 is another example of how you can cut down the wear and tear on lines or cable and reduce your frictional loss.

When you need one surface to move over another, you can decrease the friction with lubricants such as oil, grease, or soap. You can use a lubricant on flat surfaces and gun slides as well as on ball and roller bearings. A lubricant reduces frictional resistance and cuts down wear.

In many situations friction is helpful. However, many sailors have found out about this the hard way—on a wet, slippery deck. You’ll find rough grain coverings are used on some of our ships. Here you have friction working for you. It helps you to keep your footing.

EFFICIENCY

To make it easier to explain machine operations, we have neglected the effect of friction on machines up to this point. Friction happens every time two surfaces move against one another. The work used in overcoming the frictional resistance does not appear in the work output. Therefore, it’s obvious that you have to put more work into a machine than you get out of it. Thus, no machine is 100 percent efficient.

Take the jack in figure 7-6, for example. The chances are good that a 2-pound force exerted on the handle wouldn’t do the job at all. You would need a pull of at least 10 pounds. This shows that only 2 pounds out of the 10 pounds, or 20 percent of the effort, is employed to do the job. The remaining 8 pounds of effort was is in overcoming the friction in the jack. Thus, the jack has an efficiency of only 20 percent. Most jacks are inefficient. However, even with this inefficiency, it is possible to deliver a huge push with a small amount of effort.

A simple way to calculate the efficiency of a machine is to divide the output by the input and convert it to a percentage:

Now go back to the block-and-tackle problem illustrated in figure 7-5. It’s likely that instead of being able to lift the load with a 120-pound pull, the sailor would have to use a 160-pound pull through the 100 feet. You can calculate the efficiency of the rig by the following method:

and, by substitution,

Theoretically, with the mechanical advantage of 12 developed by the cable winch in figure 6-11, you can lift a 600-pound load with a 50-pound push on the handle. If the machine has an efficiency of 60 percent, how big a push would you actually have to apply? Actually, 50 + 0.60 = 83.3 pounds. You can check this yourself in the following manner:

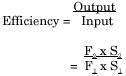
One revolution of the drum would raise the 600-pound load a distance S₂ of 2pr, or 7.85 feet. To make the drum revolve once, the pinion gear must rotate six times by the handle, and the handle must turn through a distance S₁ of 6 x 2pR, or 94.2 feet. Then, by substitution:

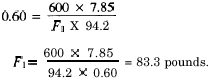
Because this machine is only 60-percent efficient, you have to put 94.2 x 83.3, or 7,847 foot-pounds, of work into it to get 4,710 foot-pounds of work out of it. The difference (7,847 – 4,710 = 3,137 foot-pounds) is used to overcome friction within the machine.

SUMMARY

Here are some of the important points you should remember about friction, work and efficiency:

You do work when you apply a force against a resistance and move the resistance.

Since force is measured in pounds and distance is measured in feet, we measure work in foot-pounds. One foot-pound of work is the result of a 1-pound force, acting against a resistance through a distance of 1 foot.

Machines help you to do work by making it possible to move a large resistance through a small distance by the application of a small force through a large distance.

Since friction is present in all machines, more work must be done on the machine than the machine actually does on the load.

You can find the efficiency of any machine by dividing the output by the input.

Friction is the resistance that one surface offers to movement over a second surface.

Friction between two surfaces depends upon the nature of the materials and the size of the forces pushing them together.